Advent of Haskell 2020: Santa Wrap

This article is part of Advent of Haskell 2020 🎄. Make sure to check the other articles too! You will find the code for this blog-post at the original GitHub publication.

Our Christmas project

Year 2020 is terrible. Santa’s Workshop had to take stay-at-home restrictions. However, Elves want to do the utmost to keep Christmas’ spirit alive. This year, Elves will work from home rather than work in the streamlined workshop 🏭 . They will get back to a more traditional way of preparing presents, like Elderly Elves who live more than 500 years, remember. In short, every Elf works in their own garage 🏠. They receive the Christmas wishlists of neighboring families: crafting toys 👾, sewing clothes 👕, or cooking delicious cookies 🍪.

One particularly annoying task for work-from-home Elves, however, is to wrap presents 🎁. They had avoided this task in the recent years thanks to automation. Elves all have different pieces of wrapping-paper at home, in particular wrapping-paper rolls vary in ratio and vary in size from one Elf to another one. Elves want some software to help them cut wrapping-paper for the presents they prepare ✂️. Some Elves have tools to cut paper (think of a cookie-cutter, but for large sheets of paper), whereas others only have cissors. Wrapping may become scarce if used inefficiently, and anyway ordering takes time. Thus, they would like to have a rough idea of how to efficiently cut the paper rolls given their own specific constraints. It does not have to be perfect, but it cannot be completely naive either. Thus, Elves need some creative idea to save Christmas’ spirit. For the better or for the worst Elves resorted to use software 💻.

Fortunately, an Elf has learnt Haskell, a language especially good for building small command line tools and with libraries to generate images. He also has learnt MiniZinc, a language especially good for solving this family of problems. Put together, these languages can help building a small tool that Elves can run at home with their own input. This computer-savvy Elf suggests the following #trade-off:

• Elves will input the quantity and shape of the wrapping for the presents (or the shape of their cookie-cutter tools that fit for the present)
• the shape of the wrapping is blocky, that is, made of various rectangle blocks, rather than arbitrarily shaped (it simplifies cutting and folding paper with rulers and guides anyway)
• Elves will also input the size of their own paper sheets
• the output is a footprint image of how to cut the paper to fit all present (when possible) Some Elves expected more specialized tools, some cared especially about saving wrapping paper. However, time is running out, our software Elf-ineer only has a day to build this software or it will be too late to save Christmas.

I am not sure I should reveal this, but, I work in Santa Incorporated oh oh oh. Do not tell your kids! in exchange I’ll explain you how I built santa-wrap in a rush to help the Elf. Thus, the main goal for this article is to relate how to iterate quickly on a practical one short day project. Secondary goals are to pike your interest about MiniZinc and introduce you a library named minizinc-process.

Approach

The type of problem for cutting wrapping paper is known as a Packing problem. These problems are generally difficult to solve efficiently. However, for small sizes or particular form of constraints, some solutions could be efficiently found (or the litterature may have some heuristics that work well empirically). Generally, the difficulty comes from integrality of constraints, that is you either can wrap a present or not wrap the present, you cannot wrap a fraction of a present. Such problems come up a lot in industrial settings where some resource is scarce. In this particular case, we cheated a bit as we came with an idea to write a blog post. However, with a bit of practice you will recognize packing problems everywhere.

We want to show off how to combine MiniZinc (a mathematical #optimization language and toolchain) with Haskell (which readers of this Advent of Haskell submission are familiar with). We will show the progression of a tool, with building a value-adding prototype in a day or two of work for some Elf familiar with Haskell and Minizinc.

Motivating our Iterations

The author built this tool in four broad iterations: implement a demo solver in MiniZinc, generate simple pictures for each wrapping, introduce the concept of layout, and, bridge the solver. We motivate each iteration before jumping into lengthier explanations.

Implemeting a solver in MiniZinc: I wanted to leverage powerful global constraints with their own heuristics/optimized solutions that exist in MiniZinc. Such a model helps us formalize the problem in better terms and understand what are inputs and what are outputs. In a business settings, such prototypes allow to raise the important questions. In that case, the whole problem is solved with a single global contraint named geost_bb. Knowing which constraints help modeling a problem is a type of expertise that takes time to acquire but that can change drastically the viability of such a tool.

Generate simple pictures: our tool needs to generate pictures of the wrapping, and I find a blog-post with picture more appealing than without. Visualizations illustrate the problem. I am not familiar with low-level graphics libraries. I typically use high-level tools for my charts like ggplot in R – they typically get in the way if what you want is pixel-perfect position of image width/height. For this exercise, I found JuicyPixels and I need to validate quickly that JuicyPixels will fit the needs. This library is appealing because I could generate PNGs with little dependencies. I had some experience with Gloss. However, I discarded this choice for I only need static images and not animations (and Gloss has way more dependencies than JuicyPixels).

Introduce the concept of layout: pictures become more interesting when we start to have multiple boxes. Once I know how to print a layout I am done with the graphical aspects of the problem. Minor improvements can still come later but it is mind-relaxing to call something done. Further, at this point it is easy to show some naive layouts.

Bridge the solver: this is the boiler-plate part of the work. minizinc-process actually have a TemplateHaskell helper to generate an input and output representations but this approach is limited: it cannot work with sets in its current version and does not preclude writing boilerplate to transform between “business-domain” representations and solver input/output representations. Plus, the goal of the article is to illustrate the pro/cons. This part of boiler-plate is the one requiring the most care, hence my usage of newtypes to differentiate indices.

Graphically, the following dependency graph shows the various steps I had in mind. 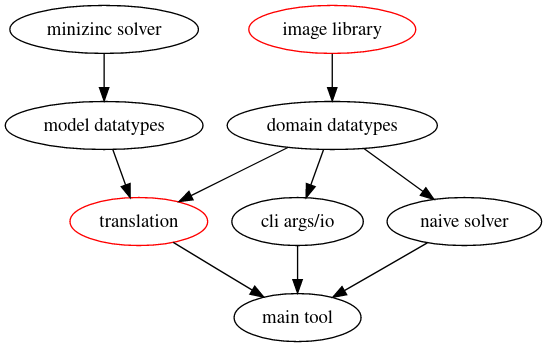In red are the two chunks of work which I assessed has being the most uncertain (i.e., requiring the most discovery) or most meticulous (i.e., spending time building accurate types to reduce the risk of bugs).

Let’s discuss how this four iterations looked like.

The four iterations

We now dive in more details into each iteration. Recall that I time-boxed this project to the equivalent of a short-day-of-work. Readers should be able to read these independently.

A solver in MiniZinc

We basically call the global contstraint geost_bb. Let’s unpack how it works, starting from a small MiniZinc overview and a mini tutorial on geost_bb.

In MiniZinc you separate the structure of a problem (which we call a model) and its particular instance (determined by input parameters). Thus a model can run for various input parameters. Further, the model separate two families of variables: the par variables (parameters that are given or can be deterministically computed from other parameters) and var variables (decisions that the solver will make). Constraints are statement that link variables together. The solver, then works out solutions (that is assignments of variables) that are consistent with all constraints. It is typically easy to verify that a given assignment matches all constraints. For instance, in our Santa-Wrap tool can visually inspect whether or not cutting guides for different present intersect. Whereas, it is typically hard to find a given assignment for all possible par inputs (or an optimal one when a criteria of goodness exists).

In Haskell parlance: solver :: Model -> Parameters -> Maybe Decisions, which, partially-applied for some Model would give solveProblem :: Parameters -> Maybe Decisions. To encode this faithfully in Haskell we would need to ensure that the Parameters and Decisions types actually depends on the Model; somehow, discussing these type-level programming techniques is out of scope for this article.

Typically, writing MiniZinc is a bit like SQL queries: you describe what you want and let the engine fetch it for you. The ability to summon a magic tool to solve our wishes comes with some limitations: expressivity is limited, and you need to be careful what you wish for. For instance, when writing MiniZinc you need to discuss about finite inputs/outputs (e.g, no unbounded recursion). Further, small changes on the structure of the problem can drastically change performance (like switching from a index scan to a table scan in SQL query plan).

The comparison with SQL does not stops at the declarative aspect. Typical domain models in Haskell have collections such as Lists or Maps or custom recursively-shaped objects etc. Once mapped into tabular form in SQL, special conversion care is required. For instance, in Haskell, a type User { age :: Int , height :: Int } would map to a set of integers (one user-id per user) and two arrays indexed by user-id. So that Haskell domain objects like these.

users :: [ User ]
users = [ User 23 172, User 45 180, User 36 165 ]

Would translate to the following MiniZinc.

set of int: USER = 1..3;
array[USER] of int: age = [ 23, 45, 36 ];
array[USER] of int: height = [ 172, 180, 165 ];

Readers familiar with Relational Algebra, DataParallel Haskell, Columnar Storage, or Entity Component System will find comonalities. We will work this out for our problem in more detail in the last iteration. So now let’s look at geost_bb.

Here is a snapshot of geost_bb documentation . Which sorts of packs blocky-structure on a multi-dimensional space. This constraint does not try to shrink gaps between objects, it “merely” (I don’t want to downplay how great this is) force assignments of variables such that no overlap exists between the packed objects.

We annotate the parameters below to explain why using this function make sense in Santa-Wrap. Besides the opaque name, it does exactly what we want to help the Elves and even a bit more.

• k: here we live in two dimensions, that an easy parameter, we’ll hardcode it
• rect_size: size of each rectangles along each dimension
• rect_offset: offset of rectangles long each dimension
• shape: wrapping shapes are built from a set of a rectangles, for instance presents we can wrap in a simple rectangle would have a single rectangle. More elaborated wrapping shapes may require two or more adjacent rectangles. For instance the sword here is built with two overlapping rectangles: a rectangle is horizontal (largest rect_size is the 1st dimension) and another rectangle is vertical (largest rect_size is the 2nd dimension) and both rectangles are translated along an axis (i.e., one non-zero rect_offset). Multiple shapes could re-use the same rectangles if they happen to match (hence, saving a bit on the complexity – but we won’t go into this level of sophistication).
• l and u: upper and lower bounds for each wrapping, in our case all objects can equally be positioned on the wrapping, hence the lower bound is 0 and the upper bound the size of the roll (minus one if you care about millimeters and took no margins of error at all in your measurements)

Then geost_bb then contributes constraints to tell the solver to make a number of decisions:

• x: the coordinates of the wrapping shapes (which are themselves built of rectangular blocks). For our sword example, we need to add the rect_offset to the x coordinate of the shape to position a rectangle.
• kind: the shape used by each object. This mechanism allows geost_bb to chose any shape for the different objects. External constraints actually prevent geost_bb does not know how many times it must be using the wrapping-shape for a sword, and unconstrained the solver would rather prefer the simpler wrapping-shape for a book. This mechanism actually is a feature: the freedom to pick among shapes allows to model rotation of shapes, we will not use this for now.

In our case, for a first version of the tool we do not need to make that many decisions: only x above is required. Declaring all inputs to give to geost_bb is required, however. We still need to actually declare our par and var variables.

We will have to discuss about a number of entities:

• two dimensions: int: nDims = 2; set of int: DIM = 1..nDims
• wrapping shapes: int: nShapes; set of int: SHAPE = 1..nShapes
• rectangular blocks: int: nBlocks; set of int: BLOCK = 1..nBlocks
• each object we need to wrap: int: nObjs; set of int: OBJ = 1..nObjs
• the roll: it is implicit that we cut one roll, so we do not need to declare anything

Then, some characteristics of entities:

• the size of the roll: int: x_max; int: y_max
• the size of individual rectangular blocks and their offsets in each dimension: array[BLOCK,DIM] of int: rect_sizes; array[BLOCK,DIM] of int: rect_offs
• the coordinates of where to position cuts for our solution: array[OBJ,DIM] of var int: coordinates

Finally there is relational information linking various entities.

• to each object we associate a given shape (present1 is a Guitar, present2 is a book etc.): array[OBJ] of SHAPE: object_shapes;
• each shape is the collage of a set of rectangle, we could use various external representation to model the set of rectangles (e.g., an array[SHAPE,RECTANGLE] of bool is isomorphic to an array[SHAPE] of set of RECTANGLE) but we will stick to the set representation that geost_bb requires (using another input would require extra constraints to link input and geost_bb representations)

All in all, the model is in models/santa-wrap.mzn and an example input for it is models/santa-wrap001.dzn. You can run it with minizinc models/santa-wrap.mzn models/santa-wrap001.dzn. And the output I got was:

coordinates = array2d(1..10, 1..2, [8, 0, 0, 6, 7, 0, 0, 5, 6, 0, 0, 4, 4, 0, 0, 2, 2, 0, 0, 0]);

Which you can read as “first object” is a (8,0), the “second object” is at (0,6) etc. Elves could work with such an output, however a visual display is better. Plus they want to prepare their cutting boards, build guides, or simply pass an eye-check that things are in the right place.

Generate simple pictures

I have had little interest in graphics in the past. Thus I vaguely know some Haskell libraries exist like diagrams, gloss, JuicyPixels, or reanimate. For this project, I had to dive a bit more and actually pick some library. My choice settled on JuicyPixel for two main reasons: on the first hand, this library has only a small amount of dependencies (especially system dependencies – gloss requires some OpenGL). On the other hand, the documentation was welcoming: I looked for IO () because I looked for some “main” or “print” equivalent. The first hit on the top module is generateImage. No kidding, here is the screenshot to prove it: first hit .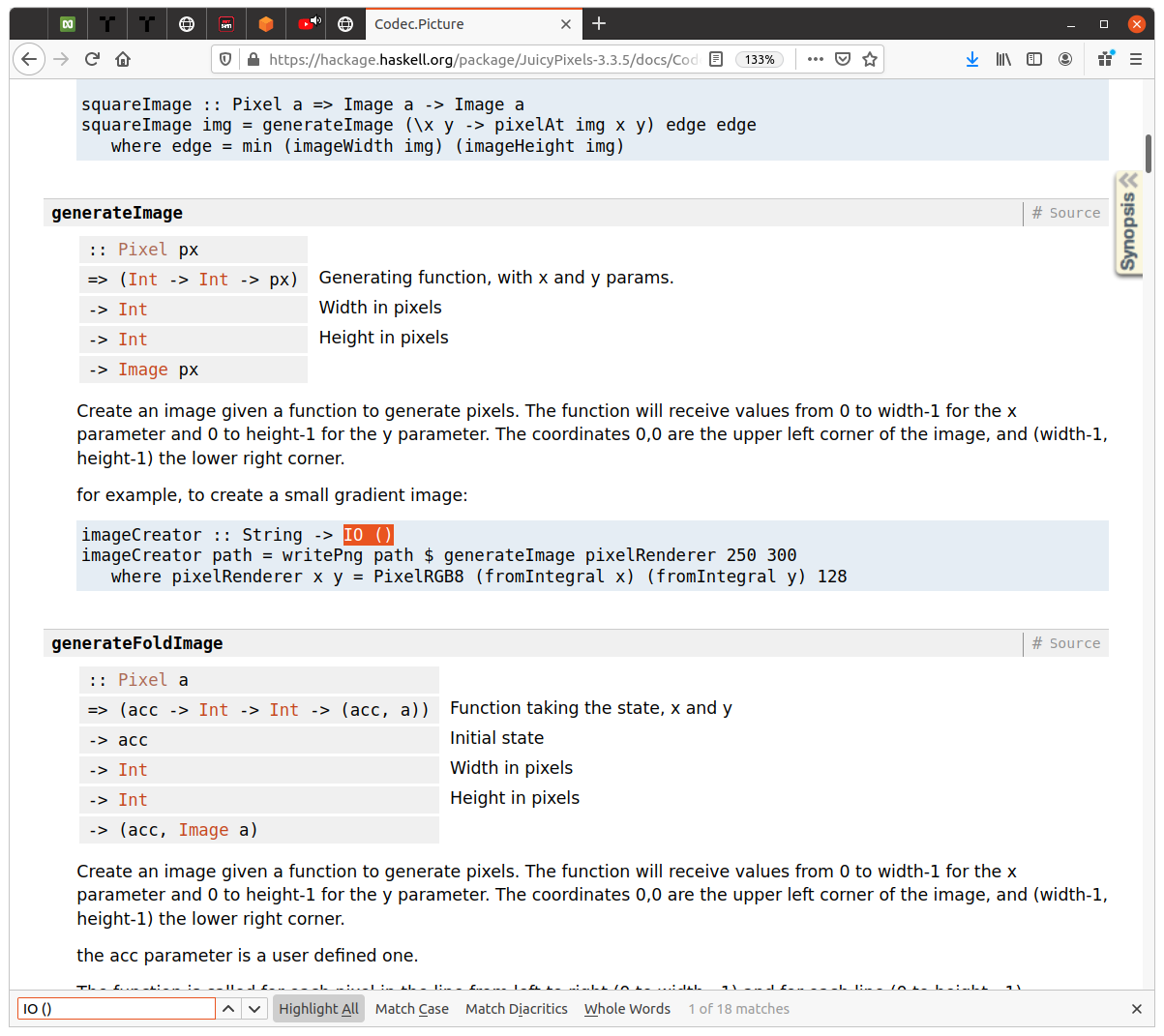

The type information tells me the library actually scans every pixel one by one. It is very likely super inefficient. That said, the cost of optimizing the packing is the major bottleneck in this problem. Elves can wait a minute to save hours. A warming case that does not corroborate the claim that Haskell libraries are poorly documente. My first action was to verify that the example actually works.

cabal repl
> import Code.Picture
> let path = "images/background.png"
> let pixelRenderer x y = PixelRGB8 (fromIntegral x) (fromIntegral y)
> writePng path $ generateImage pixelRenderer 250 300

And voila! thank you so much JuicyPixels. It’s not “too good to be true”: the example works.

Having secured that I can generate PNG, what is left? we need to define some Haskell data types to map loosely with what I’ve learnt is required in the MiniZinc optimization. However we’ll be using Haskell records rather than columnar values. The idea here is to use these data types as main Haskell types for parsing a format that Elves are likely to know such as JSON. Further we want to allow Elves to pass extra information like quantities of each present they will wrap, colors and names for pictures before crafting the guides etc.

Some excerpt:

data Wrapping = Wrapping {
    name       :: Name
  , colorNum   :: Int
  , quantity   :: Quantity
  , rectangles :: [ Rectangle ]
  } deriving (Show, Generic)
instance FromJSON Wrapping

data Rectangle = Rectangle {
    rectX :: Length
  , rectY :: Length
  , offX  :: X
  , offY  :: Y
  } deriving (Show, Generic)
instance FromJSON Rectangle

Wrappings are built of Rectangles. Each Rectangle as length/width (lengths in both dimensions rectX, rectY) as well as some offset in both dimension. In addition, each Wrapping has a name, a quantity and some color to visualize more easily a layout. But before speaking about Layouts, what we can do is to generate pictures for each Wrapping. This way, Elves can calibrate the units and verify individual length.

I need to adapt the JuicyPixels example I copy pasted to build a function printWrapping :: Wrapping -> IO(). In short, it has a Wrapping and its associated Rectangles in scope and we need to implement pixelRenderer.

So I’ll build utility functions findRectangle x y which finds a rectangle with the right sizes and offset to contain the pixel (x,y).

A single pixel and rectangle test is

rectangleContainsPixel x y rect =
  let x0 = scale $ offX rect
      x1 = scale $ offX rect + rectX rect
      y0 = scale $ offY rect
      y1 = scale $ offY rect + rectY rect
  in  x0 <= x && x < x1 && y0 <= y && y < y1

Which checks for intervals in both X and Y. The scale function just multiplies tenfold every magnitude (i.e., a dimension of 1 Length is shown with 10 pixel). With that utility function we can now test every rectangles: if some is found, we color the Pixel with some value, otherwise we use default background value.

pixelRenderer x y =
  case findRectangle x y of
    Nothing -> PixelRGB8 (fromIntegral x `mod` 32) (fromIntegral y `mod` 32) 128
    Just idx -> pixelColor idx

findRectangle x y = List.findIndex (rectangleContainsPixel x y) (rectangles wrapping)

I use List.findIndex so that on a hit i can also attribute some color (see pixelColor :: Int -> PixelRGB8 which defines a palette) and paint the rectangle in a different color.

Another utility function is needed to give JuicyPixel the size of the picture to create. This size corresponds to the farthest point in the set of off-set rectangles maxX = maximum (0 : [ rectX r + offX r | r <- rectangles wrapping ]), I named this value the extentX of a Wrapping in later commits. I use comprehension list notation. I add a 0 so that maximum does not crash on an empty list.

Our main function basically parses stdin into some [Wrapping] and traverse this list with our PNG generator.

mainParts = do
  wrappings <- eitherDecode' @[Wrapping] <$> ByteString.getContents
  case wrappings of
    Left err -> print err
    Right xs -> traverse_ printWrapping xs
  putStrLn "done!"

The parsing leverages the automatically-generated instance FromJSON from aeson (extension DeriveGeneric). Note that we use TypeApplications for the syntax @[Wrapping] which explicitates what we are decoding from the content in stdin, which also helps GHC provide less general error message when I change and break things.

This way, our main binary can generate individual images.

$ santa-wrap parts < input/wrapping001.json 
$ done!

The parts are individual .png files as this listing shows: 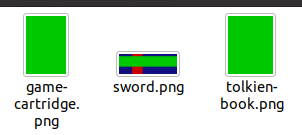. Elves can use these parts to prepare some guides to later cut wrapping paper rapidly.

Now let’s finally introduce the concept of layout.

Introduce the notion of layout

The layout is a collection of positioned wrappings. There’s an obvious Functor instance for Positioned. I could refactor Rectangle into a Positioned Rect. This way, a Layout is a [ Positioned [ Positioned Rect ] ] and it is probably collapsable into a single list by translating the inner Positioned objects. Something like flatten :: [ Positioned [ Positioned a ] ] -> [ Positioned a ] I feel tempted to actually dig in this direction. However, I’m far from done and the clock ticks. In short, I will save this for later and perform a good amount of copy-pasting.

The Haskell code is simply:

data Positioned a = Positioned {
    posX :: X 
  , posY :: Y 
  , item :: a 
  } deriving (Show, Functor)
    
data Layout = Layout {
    positionedWrappings :: [ Positioned Wrapping ]
  } deriving (Show) 

And now my printLayout function has a very similar pixelRenderer. Two distinctions though:

• to color a pixel you need to determines if a Wrapping has a Rectangle and the Rectangles are translated by posX and posY.
• we want to add a few pixels of margin so that a series of adjacent squares do not appear like a long rectangle, this small margin will ease verifying layouts at a glance.

Hence, our rectangleContainsPixel test takes all these things into account:

rectangleContainsPixel :: X -> Y -> Int -> Int -> Rectangle -> Bool
rectangleContainsPixel posx posy x y rect =
        let x0 = scale $ posx + offX rect
            x1 = scale $ posx + offX rect + rectX rect
            y0 = scale $ posy + offY rect
            y1 = scale $ posy + offY rect + rectY rect
        in  (x0 + margin) <= x && x < (x1 - margin) && (y0 + margin) <= y && y < (y1 - margin)

How do you verify that the margin is pretty enough? Simply generate a naive Layout function. We just lay out shapes left-to-right.

linearLayout :: [ Wrapping ] -> Layout
linearLayout wrappings = Layout $ List.zipWith (\w (x,y) -> Positioned x y w) wrappings xys
  where
    xys :: [(X,Y)]
    xys = List.scanl placeToTheLeft (0,0) wrappings 

    placeToTheLeft :: (X, Y) -> Wrapping -> (X, Y)
    placeToTheLeft (x,y) w = (x + extentX w, 0)

The interesting aspect is the use of List.scanl to perform a fold an accumulate intermediary values. The accumulator is the position for the next Wrapping (hence, we start at (0,0) and then we move right by an amount large enough to ensure there will be no overlap: what we named the extent of the wrapping shape.

This function does not even take care of the bounds of the roll. This function is merely useful to have some comparison point and to exercise the printLayout function.

Running the following command will give the image below.

$ santa-wrap linear-layout ./layout.png < input/wrapping003.json 
done!

Now we see the margins, the coloring. We also have a MiniZinc model for non-naive layouts. Let’s bring the two things together.

Actually bridge the Haskell and MiniZinc code

Showcasing my minizinc-process library is, a main motivator (second to saving Christmas’ spirit, though).

Remember that, we want to approach ergonomics for the solver so that in Haskell-land it feels like we have a function solver :: Model -> Parameters -> Maybe Decisions. Here enters minizinc-process, an helper library that actually uses MiniZinc support for JSON input/outputs. This is feasible with runLastMinizincJSON, which has type:

runLastMinizincJSON ::
  (ToJSON input, FromJSON answer) =>
  MiniZinc input answer ->
  input ->
  IO (Maybe answer)
runLastMinizincJSON = ...

The typeclass constraints on input and output allow to serialize back and forth using JSON. The Minizinc input answer actually contains the model (e.g., a filepath to the models/santa-wrap.mzn file) and parameters for driving MiniZinc (i.e., which solver to use, whether there is a timeout or to search forever, but also, how to create intermediary .json input files that play the role of the models/santa-wrap001.dzn for each different possible input). For this project, we use the simpleMiniZinc constructor to get a Minizincthat also adds some Hashable constraint on the input type so that we can generate filenames. Fortunately, Hashable is generically-derivable as well so little boilerplate is incured.

The runLastMinizincJSON functions runs for up to the timeout provided in the MiniZinc option and return the latest decisions (if there is any). A more general function runMinizincJSON exists. This function takes a state-machine named ResultHandler to handle individual results. Indeed, we can ask MiniZinc to return multiple solutions, prove that there are no more solutions, and handling this variety of cases asks for more complicated types.

The underlying type are:

data SearchState a
  = Exhausted a
  | Incomplete a
  | Unsatisfiable
  | InternalError String

data ResultHandler obj b
  = ResultHandler
  { handleNext :: b -> SearchState obj -> IO (b, Maybe (ResultHandler obj b))
  }

The result handler is parametrized by obj which are the decisions that the solver makes, and the handler is also parametrized by b – an accumulator state like in a fold. A handler is called each time the search changes SearchState. The handler is free to do what it wants but must return an updated state and an updated handler (or an absence of handler to tell the library that we can stop the search). Later versions of the library will likely generalize IO in the handler to some parametric class.

There is not much more to minizinc-process. Let’s use it in practice.

We need to translate two worldviews for the same information, back and forth. MiniZinc expects data in array shapes and other parameters giving the length of these arrays whereas our Haskell data is meant to help interactions with users. Hence, the Haskell datatypes closely follow Elf-semantics. Typically, translation code between two worldviews benefits from careful newtypes to distinguish array indices. Indeed, every entity becomes identified by an index and it is all too common to make an error. Multi-dimensional arrays have some support for types in MiniZinc but the data serialized in JSON do not.

The risk we want to reduce is to mix-up array indices and mix-up the terminology. This is where newtypes shine in Haskell. Two extensions, DerivingStrategies and GeneralizedNewtypeDeriving come handy to save on boilerplate.

newtype ShapeIdx = ShapeIdx Int
  deriving stock Show
  deriving stock Eq
  deriving newtype Hashable
  deriving newtype ToJSON
newtype BlockIdx = BlockIdx Int
  deriving stock Show
  deriving newtype Hashable
  deriving newtype ToJSON

We can now write an Haskell data type for the input. This data type has fields mapping closely the names of par variables in MiniZinc (which you find declared in the ./models/santa-wrap001.dzn). Arrays map to lists, two dimensional arrays become nested lists. Sets required me to define an indirection named MinizincSet (will be merged upstream) to match MiniZinc expectations for its JSON inputs. Thus, my Input and Output types become.

data Input = Input {
    nBlocks :: Int
  , rect_sizes :: [[Int]]
  , rect_offs :: [[Int]]
  , nShapes :: Int
  , shapes :: [ MinizincSet BlockIdx ]
  , nObjs :: Int
  , object_shapes :: [ ShapeIdx ]
  , x_max :: Int
  , y_max :: Int
  } deriving (Show, Generic)
instance Hashable Input
instance ToJSON Input

data Output = Output {
    coordinates :: [ (X, Y) ]
  }
  deriving (Show, Generic)
instance FromJSON Output

The rest of the work now requires to build a convertInput function that takes Haskell domain values, map that into an Input. This mapping will require to give integral IDs to entities. For instance, each individual Wrapping in the input requires as many OBJECT as the quantity requires. I typically use list-comprehensions and zipping with [1..] to achieve this indexing.

For instance, each Wrapping has one SHAPE in our problem. Thus, we provide an indexed list of shapes and its “originating” Wrapping as follows.

indexedWrappings :: [(ShapeIdx, Wrapping)]
indexedWrappings = zip (fmap ShapeIdx [1..]) wrappings

The BLOCK and their rect_sizes, rect_offs are a bit more complicated. To build everything we want, we need a “table” with, for each SHAPE, what BLOCK it is made of, and the “originating” Rectangle to get carry the sizes and offsets.

indexedRects :: [(ShapeIdx, BlockIdx, Rectangle)]
indexedRects = zipWith (\blockIdx (shapeIdx, r) ->  (shapeIdx, blockIdx, r))
  (fmap BlockIdx [ 1.. ])
  [ (shapeIdx, r) | (shapeIdx,w) <- indexedWrappings, r <- rectangles w ]

We can then compute the number of BLOCK, which is nBlocks = length indexedRects. An optimization could have been to share equal blocks when shared across SHAPEs (i.e., when a same Rectangle appears in two Wrappings). Let’s not suffer from early optimization.

We can now build the rect_sizes and rect_offs of each BLOCK by directly looking at the values associated in the “originating” Rectangle.

rect_sizes = [ [rectX r, rectY r]  | (_,_,r) <- indexedRects ]
rect_offs = [ [offX r, offY r] | (_,_,r) <- indexedRects ]

and the relational information “which SHAPE contains which BLOCK” is a reading of the ‘join’ of the indexedRects and the indexedWrappings tables. Again, we use comprehension-lists to the cardinal product of the two tables (and collecting that in MinzincSet).

shapes = [ MinizincSet
           [ blockIdx | (shapeIdx2,blockIdx,_) <- indexedRects
                      , shapeIdx1 == shapeIdx2
           ]
         | (shapeIdx1,_) <- indexedWrappings
         ]

Performance could become a concern for large amount of Wrapping and large amount of Rectangle. However, again, we are not chasing seconds in serialization/translation code as we are ready to spend minutes of solver-time to saves hours to our Elves. If data proves this piece of code is the bottleneck in practice, we can then try to optimize further this type of code. Since the code is pure, it is really amenable to property testing under QuickCheck or HedgeHog: for any data, both the (slow)-reference and (putatively-optimized)-candidate functions are returning equal outputs.

Finally, our MiniZinc model wants OBJECT, one per present rather than one per Wrapping objects (the Haskell data model holds a quantity). I mistakenly did two things at a time: expanding quantities and associating a Shape to each Wrapping. flattenedWrappings in the heat to release something early for our Elves.

flattenedWrappings :: [(ShapeIdx, Wrapping)]
flattenedWrappings = mconcat [ replicate (quantity w) (shapeIdx, w) | (shapeIdx, w) <- indexedWrappings ]

This code means that if we have Wrapping { name = abc , quantity = 2 } and Wrapping {name = def, quantity = 5} then we have to lay out seven OBJECT, two of SHAPE associated to abc and five of SHAPE associated to def. The corresponding boilerplate is:

nObjs = length flattenedWrappings
object_shapes = fmap fst flattenedWrappings

I think this covers most of the boiler-plate. Extra function arguments are the size of the roll

x_max = sizeX
y_max = sizeY

It is tempting to just write the “forward translation code” and call it a day. In reality, if you were a consumer of such a library, you would like to minimize this horrendous boiler plate, and you still need some “reverse translation code”. Be kind to your users. You have done a lot of work to create “indexed” arrays once, you’d rather not duplicate this code. Even if you do not duplicate the code, having colocated everything within the constraints of a pure function will guarantee you that no non-determinism creeps in. Hence, you should make a “reverse translation function” at the same time as you translate forward. Bonus: you can guarantee that calls of unsafe functions (like array indexing) actually are safe because you are writing the providing and consuming dynamically-shaped data at the same place.

Indeed, because we have access to flattenedWrappings our “reverse translation code” is a single line.

layoutOutput :: Output -> Layout
layoutOutput (Output coords) = Layout
    $ zipWith (\w (x,y) -> Positioned x y w) [w | (_,w) <- flattenedWrappings] coords

Writing all this boilerplate takes time (hence why I circled it red at the beginning in my dependency graph for the tasks in this project). Such translation code would be hard to generate in the general case. Hence I do not have very good solutions but to be careful and use newtype for each index. The good news, however, is that it is pretty easy to debug: generate simple cases with one then two Wrapping, observe the generated .json file.

At last we can be gratified. A simple main that ressembles the one for linearLayout allows us to generate layouts for given roll sizes.

$ santa-wrap minizinc-layout ./layout-190x150.png 190 150 < input/wrapping003.json
done!
$ santa-wrap minizinc-layout ./layout-170x160.png 170 160 < input/wrapping003.json
done!
$ santa-wrap minizinc-layout ./layout-170x159.png 170 159 < input/wrapping003.json
no layout found!

The first command greets us with the following pictur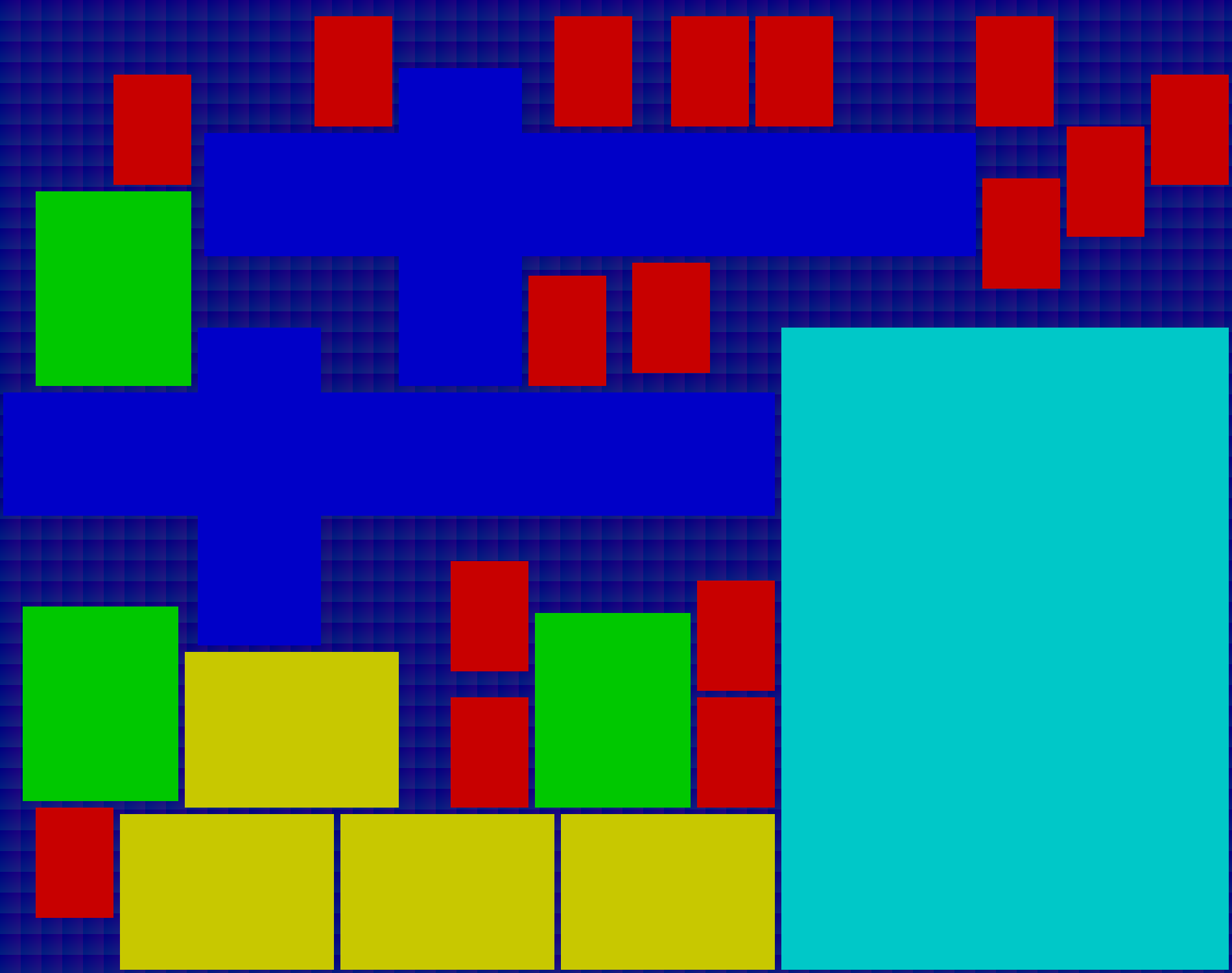e . We can try shrinking the Y-coordinates, 160 is still good, but 159 is too hard (note: it is actually infeasible but the runLastMinizincJSON function makes no distinctions between timeout and unfeasible). Visual inspection of the Y=160 case seems to show that the two cross-shaped and the big rectangle are the main reasons to limit the roll size .

Convince yourself with this picture (done by modifying the input JSON to delete everything but the shoes and the sword entries: .

OK, with this santa-wrap tool, Elves are in good shape to save Christmas’ spirit. Thank you MiniZinc and Haskell!

For the fun try packing that yourselves (input is input/wrapping005.json)

Discussion

Given more times, a number of possible improvements could happen. For a work project more discussions with the Elves would help adding more constraints to the Model. We next discuss some possible “improvements”.

Possible improvements

Elves have deadlines too, although they would love to keep improving their tools, they have other important (albeit slightly more mundane) tasks at their day jobs. Besides the discussion about Positioned being an interesting abstraction, I want to discuss improvements to the solver/problem itself and illustrate how business ideas are generated/pruned with such discussions.

A user may suggest improvements to the tool, but not all improvements are equally easy to introduce. Here are a few options:

• easy: reduce some cost (material spent) ; you would need to change the satisfyability into some optimiziation trying to minimize the area bounded by maximum X-Y coordinates
• medium: pick an orientation (left-right vs. up-down) ; you would need to change Input, Output, and the model to tell which shapes an object can take, but geost already takes care of that
• hard: attribute multiple rolls at once ; you would need to change Input, Output, and the model to pass a number rolls (maybe to each one their size) and modify the MiniZinc model to decide a roll for each object; you’d generate two pictures per problem
• crazy-hard: time taken to cut with cissors ; you would need to significantly alter the model to express the notion of “gaps” or “external”.

In a typical setup I would propose to deliver the easy and medium improvements before calling the tool done. I would suggest to propose the hard improvement as more data is generated to understand if Elves actually would benefit from such changes. I would root against the crazy hard, and even propose to equip Elves with cutting-tools and drop cissors would probably use total surface as a good enough proxy, simulators can help assess how bad.

Elves would love to hear about your improvement suggestions or merge requests! Feel free to contact me or to open some Issues to discuss them together.

Epilogue

Alright, this blog post was longer than I expected. I wanted to show how Haskell can be used to solve a very practical problem and also put onto words some “tactical thinking” to avoid losing time on the less-important aspects (the one I have not circled red in my dependency diagram). My main challenge was to time-box my work to one day of code: on top of my Elvish missions I have a day job and all-in-all this is a good constraint to simulate a real-world situation. The information I had before starting: I knew JuicyPixels existed but had never used it before, I sort of framed the Santa-Wrap problem to illustrate a non-trivial MiniZinc global (geost_bb arguably is pretty advanced). I built the minizinc-process library and wanted a pretext to show-case it. I could have taken a shortcut as minizinc-process offers some TemplateHaskell to generate Input and Output datatypes (with no newtypes and no support for sets, the pedagogy would have suffered).

An advantage of the Haskell + MiniZinc combination is to be able to use each tool for what they are best at. Haskell allows me to write solid backend services and command line tools whereas MiniZinc allows me to model using MiniZinc IDE (e.g., with a nice syntax for multi-dimensional arrays). In this setup the key difficulty is the boilerplate code required to translate inputs and outputs.

I hope this article piqued your interest. Feel free to contact me if you are curious whether these types of techniques are a good fit for you. I gave a presentation of MiniZinc at an online event this year, and you will find much more on the website and on the Coursera lessons (time consuming).

Thanks to Advent of Haskell organizers and all the other articles authors.

I wish you all the best for the end of 2020 and cheers to a better 2021!

Oh oh oh!